Cho đến nay, một số lượng lớn các thuật toán ML đã được phát triển và nhiều thuật toán khác đang được nghiên cứu và phát minh với tốc độ nhanh chóng bởi giới học thuật cũng như ngành công nghiệp. Phần này sẽ xem xét một số thuật toán học sâu và truyền thống phổ biến cũng như cách áp dụng các thuật toán này cho các loại vấn đề học máy khác nhau. Trước tiên, chúng ta sẽ thảo luận về những cách chọn thuật toán ML cho nhiệm vụ phù hợp.
Lựa chọn thuật toán ML
Có một số điều cần cân nhắc khi chọn thuật toán ML cho các nhiệm vụ khác nhau:
- Kích thước dữ liệu đào tạo (Training Data Set): Một số thuật toán ML, chẳng hạn như thuật toán học sâu (Deep learning), có thể hoạt động rất tốt và tạo ra các mô hình có độ chính xác cao, nhưng chúng yêu cầu số lượng lớn dữ liệu đào tạo. Các thuật toán ML truyền thống, chẳng hạn như mô hình tuyến tính, có thể hoạt động hiệu quả khi tập dữ liệu nhỏ nhưng không thể tận dụng các tập dữ liệu lớn một cách hiệu quả như thuật toán mạng thần kinh học sâu. Các thuật toán ML truyền thống yêu cầu con người trích xuất và thiết kế các features đầu vào hữu ích từ dữ liệu huấn luyện để huấn luyện mô hình. Khi kích thước của dữ liệu đào tạo trở nên lớn, việc trích xuất và thiết kế các features hữu ích để cải thiện hiệu suất mô hình trở nên khó khăn hơn. Đây là một trong những lý do khiến các thuật toán ML truyền thống không thể tận dụng các tập dữ liệu lớn. Mặt khác, các thuật toán học sâu có thể tự động trích xuất các features từ dữ liệu đào tạo.
- Độ chính xác và khả năng diễn giải: Một số thuật toán ML, chẳng hạn như thuật toán học sâu, có thể tạo ra các mô hình có độ chính xác cao, chẳng hạn như mô hình xử lý ngôn ngữ tự nhiên (Natural language processing - NLP) hoặc thị giác máy tính (Computer Vision). Tuy nhiên, những thuật toán này có thể rất phức tạp và khó giải thích hơn. Một số thuật toán đơn giản hơn, chẳng hạn như hồi quy tuyến tính (sẽ được đề cập sau), có thể dễ dàng diễn giải mặc dù độ chính xác có thể không cao như các mô hình học sâu.
- Thời gian đào tạo: Các thuật toán khác nhau có tốc độ đào tạo khác nhau trên cùng một tập dữ liệu. Các mô hình đơn giản, chẳng hạn như mô hình tuyến tính, sẽ đào tạo nhanh hơn, trong khi các mô hình học sâu sẽ mất nhiều thời gian hơn để đào tạo.
Có một vài phương pháp định lượng cho độ phức tạp của thuật toán. Độ phức tạp về thời gian mô tả thời gian tính toán/các thao tác cần thiết để chạy thuật toán ML và độ phức tạp về không gian là dung lượng bộ nhớ điện toán cần thiết để chạy thuật toán. Big O là một ký hiệu để mô tả độ phức tạp của thời gian và không gian, xác định giới hạn ước tính của một thuật toán. Ví dụ: độ phức tạp về thời gian cho tìm kiếm tuyến tính là 0(N) và độ phức tạp về thời gian cho tìm kiếm nhị phân sẽ được biểu thị bằng 0(log (N)), trong đó N là số lượng mẫu dữ liệu trong danh sách mục tiêu.
- Tính tuyến tính của dữ liệu: Đối với dữ liệu có mối quan hệ tuyến tính giữa dữ liệu đầu vào và dữ liệu đầu ra, các mô hình tuyến tính có thể hoạt động khá tốt. Tuy nhiên, đối với tập dữ liệu có mối quan hệ phi tuyến tính (nghĩa là biến đầu vào và biến đầu ra không thay đổi theo tỷ lệ), các mô hình tuyến tính không phải lúc nào cũng có thể nắm bắt được các mối quan hệ nội tại sâu sắc hơn và chúng ta thường cần các thuật toán như mạng lưới thần kinh học sâu và cây quyết định để xử lý các bộ dữ liệu phức tạp.
- Số lượng features: Tập dữ liệu huấn luyện có thể chứa một số lượng lớn các features và không phải tất cả chúng đều phù hợp với việc huấn luyện mô hình. Một số thuật toán ML có thể xử lý tốt các features không liên quan hoặc nhiễu và một số thuật toán khác có thể bị ảnh hưởng tiêu cực đến tốc độ đào tạo hoặc hiệu suất mô hình với nhiều features không liên quan hoặc nhiễu trong quá trình đào tạo. Các thuật toán khác nhau có các cách tiếp cận khác nhau để giảm ảnh hưởng của các features nhiễu hoặc không có thông tin thông qua một kỹ thuật gọi là chuẩn hóa. Một số kỹ thuật chuẩn hóa hoạt động bằng cách thêm các thuật ngữ lỗi bổ sung vào hàm mất mát trong quá trình đào tạo để giảm ảnh hưởng của dữ liệu nhiễu. Các phương pháp khác, chẳng hạn như loại bỏ, loại bỏ ngẫu nhiên các nút trong mạng thần kinh để đạt được sự chuẩn hóa.
Chúng ta đã xem xét một số phương pháp để chọn các thuật toán ML. Tiếp theo, hãy đi sâu vào các loại thuật toán khác nhau theo các vấn đề mà chúng giải quyết.
Các thuật toán cho các bài toán phân loại và hồi quy
Phần lớn các vấn đề học máy mà thế giới hiện đang giải quyết là các vấn đề phân loại và hồi quy. Trong mục này, chúng ta sẽ xem xét một số thuật toán phân loại và hồi quy phổ biến.
Thuật toán hồi quy tuyến tính
Các thuật toán hồi quy tuyến tính được thiết kế để giải các bài toán hồi quy và dự đoán một giá trị liên tục khi cho trước một tập hợp các đầu vào độc lập. Loại thuật toán này được sử dụng rộng rãi trong các ứng dụng thực tế, chẳng hạn như ước tính doanh số bán sản phẩm dưới dạng hàm của giá sản phẩm hoặc hiểu được năng suất của một loại cây trồng như là một kết quả dựa trên lượng mưa và phân bón.
Hồi quy tuyến tính sử dụng hàm tuyến tính của một tập hợp các hệ số và biến đầu vào để dự đoán đầu ra vô hướng. Công thức cho hồi quy tuyến tính được viết như sau:
$f(x) = W_1 X_1+W_2 X_2+...+W_n X_n + \varepsilon$
Ở đây, X là biến đầu vào, W là hệ số và $\varepsilon$ là số hạng sai số. Cơ sở đằng sau hồi quy tuyến tính là đối với một tập dữ liệu trong đó đầu ra có mối quan hệ tuyến tính với các đầu vào của nó, giá trị đầu ra của nó có thể được ước tính bằng tổng trọng số của các đầu vào. Trực giác đằng sau hồi quy tuyến tính là tìm một đường hoặc siêu phẳng có thể ước tính giá trị cho một tập hợp các giá trị đầu vào. Hồi quy tuyến tính có thể hoạt động hiệu quả với các tập dữ liệu nhỏ. Nó cũng rất dễ diễn giải, nghĩa là bạn có thể sử dụng hệ số để hiểu mức độ của mối quan hệ giữa biến đầu vào và phản hồi đầu ra. Tuy nhiên, vì nó là một mô hình tuyến tính nên nó không hoạt động tốt khi tập dữ liệu phức tạp với các mối quan hệ phi tuyến tính. Hồi quy tuyến tính cũng giả định các features đầu vào độc lập lẫn nhau (không có tính tuyến tính cao), nghĩa là giá trị của một feature không ảnh hưởng đến giá trị của một feature khác. Khi có sự đồng tuyến tính giữa các features đầu vào, thật khó để tin tưởng vào tầm quan trọng của các feature tương quan.
Thuật toán hồi quy logistic
Thuật toán hồi quy logistic thường được sử dụng cho các nhiệm vụ phân loại nhị phân (Ví dụ: 0-1). Các ví dụ thực tế về việc sử dụng hồi quy logistic bao gồm dự đoán khả năng ai đó nhấp vào quảng cáo hoặc liệu ai đó có thể đủ điều kiện vay tiền hay không.
Hồi quy logistic mô hình hóa xác suất của một tập hợp dữ liệu đầu vào thuộc về một lớp hoặc sự kiện, chẳng hạn như gian lận giao dịch hoặc vượt qua/không đạt một kỳ thi. Nó cũng là một mô hình tuyến tính như hồi quy tuyến tính và đầu ra của nó là sự kết hợp tuyến tính của các đầu vào khác nhau. Tuy nhiên, vì hồi quy tuyến tính không phải lúc nào cũng tạo ra một số từ 0 đến 1 (khi cần cho xác suất), nên hồi quy logistic được sử dụng để trả về giá trị từ 0 đến 1 để biểu thị xác suất. Biểu diễn đằng sau hồi quy logistic là tìm một đường thẳng hoặc mặt phẳng/siêu phẳng có thể phân tách rõ ràng hai tập hợp điểm dữ liệu càng nhiều càng tốt. Công thức sau đây là hàm cho hồi quy logistic, trong đó X là tổ hợp tuyến tính của các biến đầu vào $B+XW^{-1}$. Ở đây, W là hệ số hồi quy:
$f(x) = \frac{1}{1+e^{-x}}$
Tương tự như hồi quy tuyến tính, lợi thế của hồi quy logistic là tốc độ đào tạo nhanh và khả năng diễn giải của nó. Hồi quy logistic là một mô hình tuyến tính, vì vậy nó không thể được sử dụng cho các bài toán với các mối quan hệ phi tuyến tính phức tạp.
Thuật toán cây quyết định
Cây quyết định được sử dụng rộng rãi trong nhiều trường hợp sử dụng ML trong thế giới thực, chẳng hạn như dự đoán bệnh tim, tiếp thị mục tiêu và dự đoán khoản vay vỡ nợ. Chúng có thể được sử dụng cho cả bài toán phân loại và hồi quy.
Cơ sở đằng sau cây quyết định là dữ liệu có thể được phân chia bằng cách sử dụng các quy tắc theo cách phân cấp, do đó, các điểm dữ liệu tương tự sẽ đi theo một đường dẫn quyết định tương tự. Cụ thể, nó hoạt động bằng cách chia nhỏ dữ liệu đầu vào bằng các features khác nhau ở các nhánh khác nhau của cây. Ví dụ: nếu tuổi là một feature được sử dụng để phân tách tại một nhánh, thì hãy sử dụng kiểm tra có điều kiện (chẳng hạn như tuổi > 50 ) để phân tách dữ liệu tại một nhánh. Nó đưa ra quyết định về feature nào và vị trí phân tách bằng cách sử dụng các thuật toán khác nhau, chẳng hạn như chỉ số Gini (chỉ số Gini đo xác suất của một biến được phân loại không chính xác) và thông tin thu được (Information gain - Thông tin thu được tính toán mức giảm entropy trước và sau khi tách ra).
Ý tưởng chính của thuật toán là thử các tùy chọn và điều kiện tách cây khác nhau, tính toán các giá trị số liệu khác nhau (chẳng hạn như information gain) của các tùy chọn tách khác nhau và chọn một tùy chọn cung cấp giá trị tối ưu (ví dụ: information gain cao nhất). Khi thực hiện dự đoán, dữ liệu đầu vào sẽ đi qua cây dựa trên logic phân nhánh đã học được trong giai đoạn học và nút cuối (còn được gọi là nút lá) sẽ xác định dự đoán cuối cùng. Xem hình sau để biết cấu trúc mẫu của cây quyết định:
Ưu điểm của cây quyết định so với hồi quy tuyến tính và hồi quy logistic là khả năng xử lý các tập dữ liệu lớn với các mối quan hệ phi tuyến tính phức tạp và tính đồng tuyến tính (co-linear) giữa các features đầu vào.
Cây quyết định hoạt động tốt với dữ liệu mà không cần xử lý trước (Pre-processing) nhiều và có thể sử dụng các giá trị phân loại và giá trị số như ban đầu. Nó cũng có thể xử lý các feature bị thiếu và sự khác biệt lớn giữa các feature khác nhau trong bộ dữ liệu. Cây quyết định cũng dễ giải thích vì nó sử dụng các điều kiện để phân chia dữ liệu nhằm đưa ra quyết định và đường dẫn quyết định cho một dự đoán riêng lẻ có thể dễ dàng hình dung và phân tích. Nó cũng là một thuật toán có tốc độ học cao. Về mặt tiêu cực, một cây quyết định có thể dễ sinh ra ngoại lệ và Overfitting. Overfitting là một vấn đề đào tạo mô hình trong đó mô hình ghi nhớ dữ liệu đào tạo và không khái quát tốt trên dữ liệu không nhìn thấy, đặc biệt là với dữ liệu có số lượng lớn các features và nhiễu.
Một nhược điểm quan trọng khác đối với cây quyết định và các thuật toán dựa trên cây nói chung là chúng không thể ngoại suy bên ngoài các đầu vào mà chúng đã được đào tạo. Ví dụ: nếu bạn có một mô hình dự đoán giá nhà đất dựa trên diện tích mét vuông và dữ liệu đào tạo của bạn chứa phạm vi từ 500 đến 3.000 mét vuông, cây quyết định sẽ không thể ngoại suy bên ngoài 3.000 mét vuông, trong khi mô hình tuyến tính sẽ bắt kịp ngoại suy này.
Thuật toán rừng ngẫu nhiên (Random Forest)
Thuật toán rừng ngẫu nhiên được sử dụng rộng rãi trong các ứng dụng trong thế giới thực cho thương mại điện tử, chăm sóc sức khỏe và tài chính cho các tác vụ phân loại và hồi quy. Ví dụ về các nhiệm vụ bao gồm các quyết định bảo lãnh phát hành bảo hiểm, dự đoán dịch bệnh, dự đoán khả năng thanh toán khoản vay và tiếp thị mục tiêu.
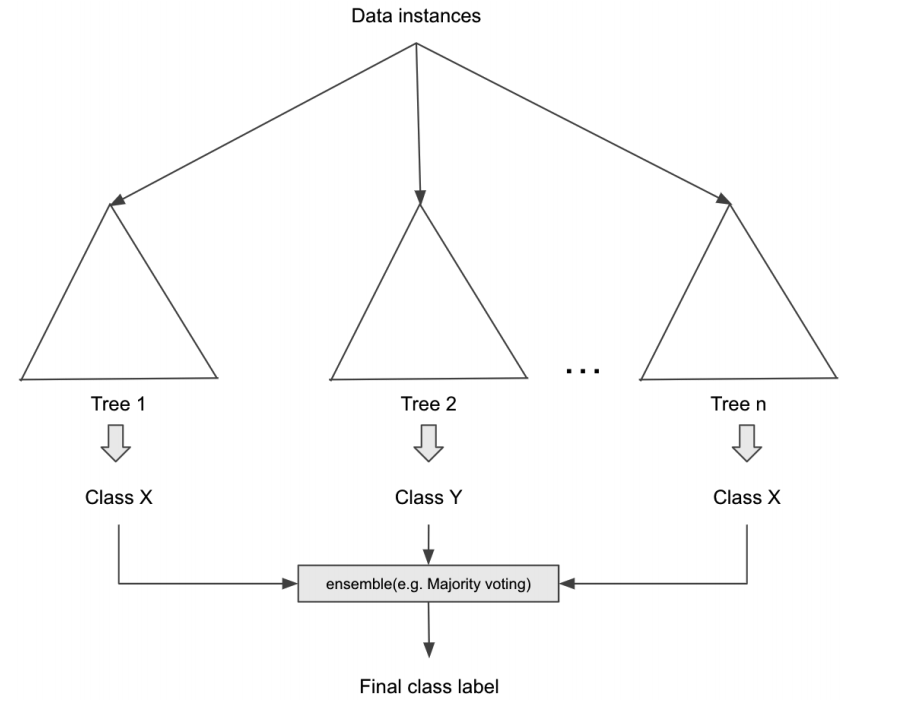
Như chúng ta đã đọc trong phần cây quyết định, cây quyết định sử dụng một cây duy nhất để đưa ra quyết định của nó và nút gốc của cây (tính năng đầu tiên để tách cây) có ảnh hưởng lớn nhất đến quyết định cuối cùng. Cơ sở đằng sau thuật toán rừng ngẫu nhiên là nhiều cây có thể đưa ra quyết định cuối cùng tốt hơn. Cách thức hoạt động của một rừng ngẫu nhiên là tạo ra nhiều cây con nhỏ hơn, còn được gọi là cây học yếu hơn, trong đó mỗi cây con sử dụng một tập hợp con ngẫu nhiên của tất cả các features để đưa ra quyết định và quyết định cuối cùng được đưa ra bằng biểu quyết đa số (để phân loại) hoặc tính trung bình (đối với hồi quy). Quá trình kết hợp quyết định từ nhiều mô hình này còn được gọi là học tập đồng bộ (Ensemble learning). Thuật toán rừng ngẫu nhiên cũng cho phép bạn giới thiệu các mức độ ngẫu nhiên khác nhau, chẳng hạn như lấy mẫu bootstrap (sử dụng cùng một mẫu nhiều lần trong một cây) để làm cho mô hình trở nên tổng quát hơn và ít bị Overfitting. Hình dưới đây cho thấy cách thuật toán rừng ngẫu nhiên xử lý các trường hợp dữ liệu đầu vào bằng cách sử dụng nhiều cây con và kết hợp các kết quả đầu ra từ các cây con:
Có một số lợi thế khi sử dụng rừng ngẫu nhiên so với cây quyết định thông thường, chẳng hạn như xử lý song song trên nhiều máy và khả năng xử lý các ngoại lệ và bộ dữ liệu mất cân bằng. Nó cũng có thể xử lý tập dữ liệu kích thước cao hơn nhiều vì mỗi cây sử dụng một tập hợp con các features. Một khu rừng ngẫu nhiên hoạt động tốt với các bộ dữ liệu ồn ào (bộ dữ liệu chứa các features vô nghĩa hoặc giá trị bị hỏng). Nó ít có khả năng làm overfitting do nhiều cây đưa ra quyết định một cách độc lập. Tuy nhiên, vì nó sử dụng nhiều cây để đưa ra quyết định nên khả năng diễn giải của mô hình bị ảnh hưởng một chút so với cây quyết định thông thường mà chúng ta có thể dễ dàng hình dung. Nó cũng chiếm nhiều bộ nhớ hơn vì nó tạo ra nhiều cây hơn, điều này sẽ ảnh hưởng đến thời gian huấn luyện mô hình.
Máy tăng cường Gradient và thuật toán XGBoost
Tăng cường gradient (Gradient boosting) và XGBoost cũng là các thuật toán ML dựa trên nhiều cây. Chúng đã được sử dụng rộng rãi cho nhiều trường hợp sử dụng như chấm điểm tín dụng, phát hiện gian lận và dự đoán yêu cầu bảo hiểm. Trong khi một khu rừng ngẫu nhiên tổng hợp kết quả ở cuối bằng cách kết hợp các kết quả từ các cây học yếu hơn, tăng cường gradient tổng hợp các kết quả từ các cây khác nhau một cách tuần tự.
Một khu rừng ngẫu nhiên được xây dựng dựa trên ý tưởng về những người học yếu hơn độc lập song song. Cơ sở để tăng cường gradient dựa trên khái niệm về cây học yếu hơn tuần tự sửa chữa thiếu sót (lỗi) của cây yếu hơn trước đó. Tăng cường gradient có nhiều siêu tham số để điều chỉnh hơn một khu rừng ngẫu nhiên và có thể đạt được hiệu suất cao hơn khi được điều chỉnh chính xác. Tăng cường gradient cũng hỗ trợ các hàm mất mát tùy chỉnh để giúp bạn linh hoạt trong việc lập mô hình cho các ứng dụng trong thế giới thực. Hình dưới đây cho thấy cây tăng cường gradient hoạt động như thế nào:

Tăng cường gradient hoạt động tốt với các bộ dữ liệu mất cân bằng và nó phù hợp với các trường hợp thực tế như quản lý rủi ro và phát hiện gian lận trong đó tập dữ liệu có xu hướng mất cân bằng. Một thiếu sót lớn của việc tăng cường gradient là nó không song song hóa khi nó tạo ra các cây một cách tuần tự. Nó cũng dễ bị nhiễu, chẳng hạn như các ngoại lệ trong dữ liệu và có thể dễ dàng overfitting do điều này. Tăng cường gradient khó diễn giải hơn so với cây quyết định, nhưng điều này có thể dễ dàng khắc phục bằng các công cụ như tầm quan trọng của biến (feature importance).
XGBoost là một triển khai của phương pháp tăng cường gradient. Nó đã trở nên rất nổi tiếng nhờ chiến thắng trong nhiều cuộc thi Kaggle. Nó sử dụng cùng một khái niệm cơ bản để xây dựng và điều chỉnh các cây, nhưng cải thiện khi tăng cường gradient bằng cách cung cấp hỗ trợ đào tạo một cây trên nhiều lõi và nhiều CPU để có thời gian đào tạo nhanh hơn, các kỹ thuật chuẩn hóa đào tạo mạnh mẽ hơn để giảm độ phức tạp của mô hình, và chống lại việc trang bị overfitting. XGBoost cũng tốt hơn trong việc xử lý các bộ dữ liệu thưa thớt. Ngoài XGBoost, còn có các biến thể phổ biến khác của cây tăng cường gradient, chẳng hạn như LightGBM và CatBoost.
Thuật toán K-nearest neighbor
K-nearest neighbor (K-NN) là một thuật toán phân loại và hồi quy đơn giản. Nó cũng là một thuật toán phổ biến để triển khai các hệ thống tìm kiếm và hệ thống đề xuất (Recommendation system).
Cơ sở cơ bản mà K-NN hoạt động theo là những thứ tương tự có khoảng cách gần nhau. Cách để xác định khoảng cách là đo khoảng cách giữa các điểm dữ liệu khác nhau. Đối với các tác vụ phân loại, trước tiên K-NN nhận dữ liệu và nhãn lớp tương ứng của chúng. Khi chúng ta cần phân loại một điểm dữ liệu mới, trước tiên chúng ta tính toán khoảng cách của nó, ví dụ: khoảng cách Euclide đến các điểm dữ liệu khác. Sau đó, chúng ta truy xuất nhãn lớp cho K điểm dữ liệu gần nhất (K trong K-NN) và sử dụng biểu quyết đa số (nhãn thường xuyên nhất trong số K điểm dữ liệu hàng đầu) để xác định nhãn lớp cho điểm dữ liệu mới. Giá trị vô hướng được dự đoán sẽ là giá trị trung bình của K điểm dữ liệu gần nhất hàng đầu cho các tác vụ hồi quy.
K-NN sử dụng đơn giản và không cần huấn luyện hoặc điều chỉnh mô hình bằng siêu tham số ngoài việc chọn số lân cận (K). Các điểm dữ liệu được nhận vào đơn giản trong thuật toán K-NN. Kết quả của nó có thể dễ dàng giải thích được, vì mỗi dự đoán có thể được giải thích bằng các thuộc tính của các lân cận gần nhất. Ngoài phân loại và hồi quy, nó cũng có thể được sử dụng để tìm kiếm. Tuy nhiên, mô hình ngày càng phức tạp khi số lượng điểm dữ liệu tăng lên và mô hình có thể trở nên chậm hơn đáng kể với một tập dữ liệu lớn để dự đoán. Nó cũng không hoạt động tốt khi kích thước tập dữ liệu cao và nó nhạy cảm với dữ liệu nhiễu và dữ liệu bị thiếu. Các ngoại lệ sẽ cần phải được loại bỏ và dữ liệu bị thiếu sẽ cần phải được quy nạp.
Tôi xin kết thúc phần 1 tại đây, phần 2 chúng ta sẽ đi sâu vào deep learning và các thuật toán khác.