Hồi quy tuyến tính
Hồi quy tuyến tính
Hồi quy tuyến tính đơn biến
Mô hình dự đoán sử dụng các thuật toán học máy, trong đó máy tính học từ dữ liệu giống như con người học từ chính kinh nghiệm của mình. Học máy có thể được áp dụng rộng rãi trong công nghiệp. Các mô hình học máy có thể được phân loại thành ba loại sau dựa trên nhiệm vụ thực hiện và bản chất của đầu ra:
Hồi quy: Biến đầu ra cần được dự đoán là một biến liên tục, ví dụ như điểm số của một học sinh.
Phân loại: Biến đầu ra cần được dự đoán là một biến danh mục (phân loại), ví dụ như phân loại email đến là thư rác hoặc thư thường.
Phân cụm: Không có nhãn được xác định trước cho các nhóm/cụm được hình thành, ví dụ như phân khúc khách hàng để tạo ưu đãi giảm giá.
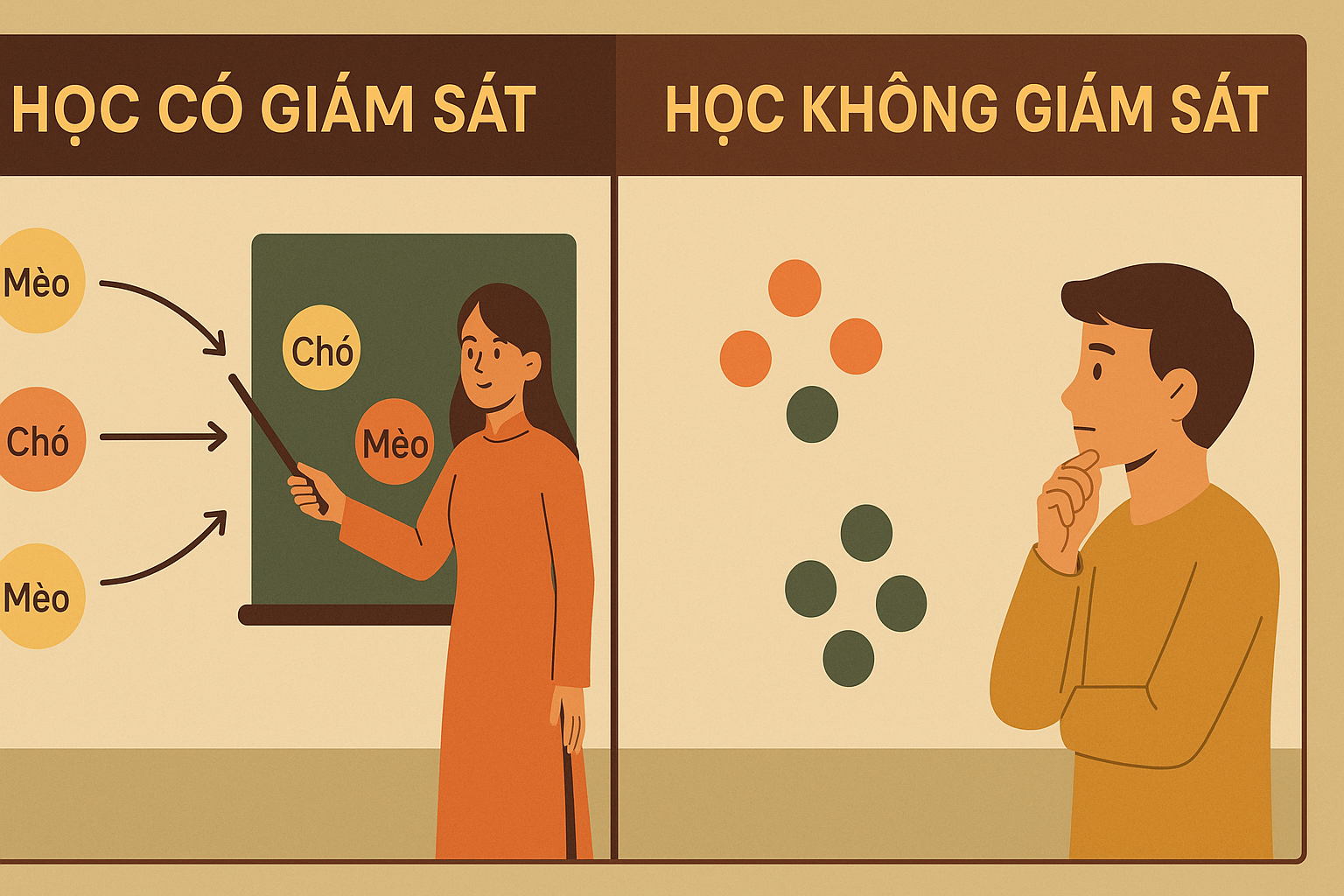
Hồi quy và phân loại thuộc vào phương pháp học có giám sát – trong đó bạn có dữ liệu từ các năm trước kèm nhãn và sử dụng chúng để xây dựng mô hình. Phân cụm thuộc vào phương pháp học không giám sát – trong đó không có khái niệm nhãn được xác định trước.
Hình 1 – Phương pháp học có giám sát và không giám sát
Hồi quy là mô hình phân tích dự đoán được sử dụng phổ biến nhất. Như bạn có thể đoán, việc dự đoán chính xác các kết quả trong tương lai có ứng dụng trên khắp các lĩnh vực – từ kinh tế, tài chính, kinh doanh, y học, kỹ thuật, giáo dục cho đến cả thể thao và giải trí. Với phạm vi ứng dụng rộng rãi và tầm quan trọng then chốt của nó, việc tìm hiểu cách xây dựng các mô hình dự đoán chính xác kết quả tương lai sẽ rất thú vị.
Trong phần này, bạn đã tìm hiểu về một lớp thuật toán học có giám sát quan trọng gọi là hồi quy tuyến tính. Ngày nay, thuật ngữ "hồi quy" thường xuất hiện khi đọc tin tức hoặc các bài báo liên quan đến thị trường chứng khoán, tài chính, thậm chí trong kinh doanh. Thuật ngữ này còn xuất hiện phổ biến trên các kênh truyền hình, chẳng hạn như khi dự đoán kết quả thăm dò sau bầu cử trước khi kết quả chính thức được công bố.
Theo khuôn khổ CRISP-DM mà chúng ta đã học, trước khi phát triển bất kỳ mô hình dự đoán nào, đầu tiên bạn phải xác định mục tiêu kinh doanh của mình và tiến hành chuẩn bị dữ liệu tương ứng (như bạn đã tìm hiểu trong mô-đun chuẩn bị dữ liệu). Trong mô-đun này, trọng tâm chủ yếu là dự đoán kết quả tương lai bằng cách sử dụng các khái niệm về hồi quy tuyến tính. Nói một cách rộng hơn, đây là một dạng kỹ thuật mô hình dự đoán cho chúng ta biết mối quan hệ giữa biến phụ thuộc (biến mục tiêu) và các biến độc lập (biến dự báo).
Bạn đã được học về hai loại hồi quy tuyến tính trong mô-đun này:
Hồi quy tuyến tính đơn
Hồi quy tuyến tính đa biến
1. Hồi quy tuyến tính đơn biến
Loại mô hình hồi quy cơ bản nhất chính là hồi quy tuyến tính đơn biến, giải thích mối quan hệ giữa một biến phụ thuộc và một biến độc lập bằng một đường thẳng. Đường thẳng này được vẽ trên biểu đồ phân tán của hai biến đó.
Hình 2 – Biểu đồ phân tán
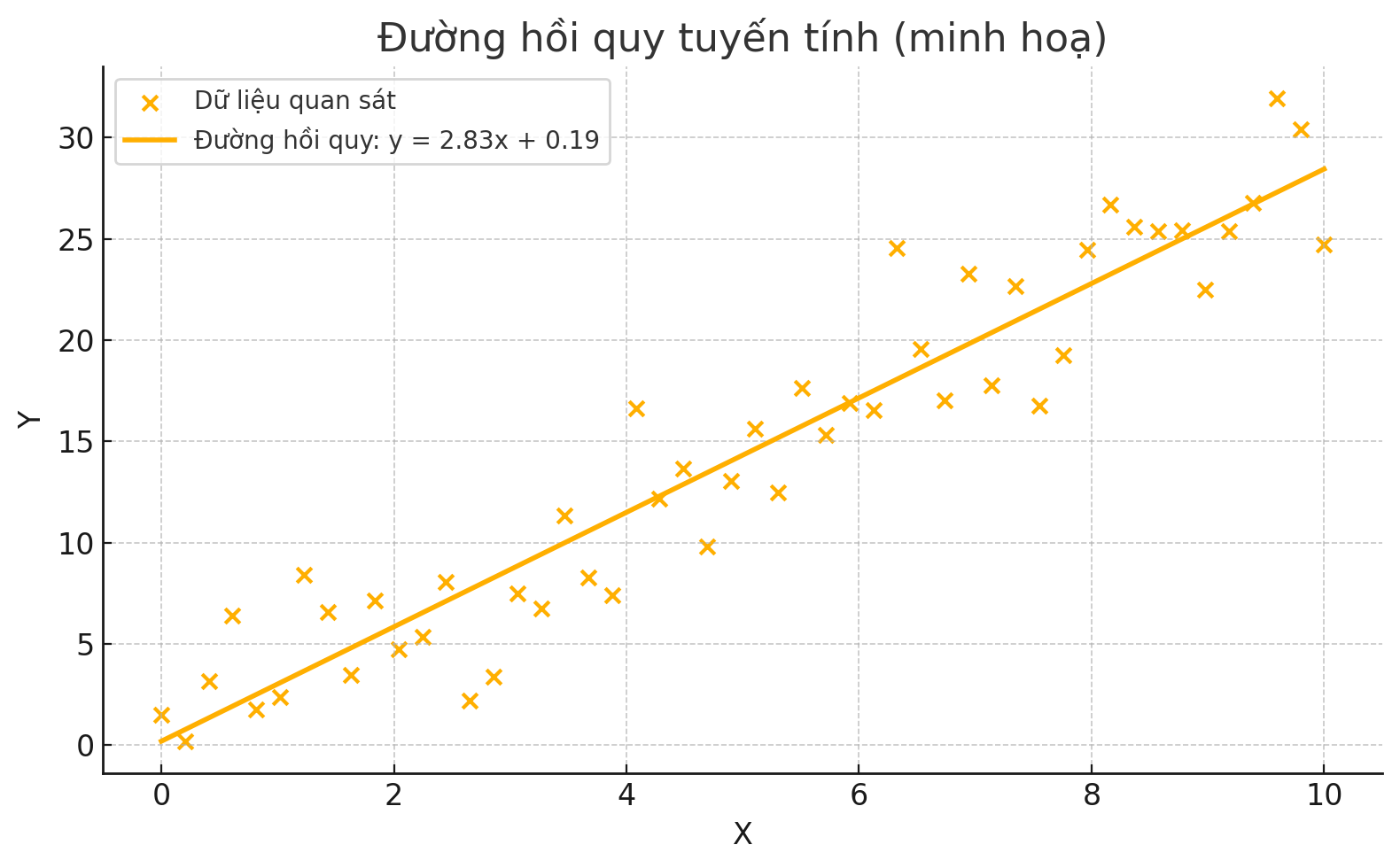
Phương trình chuẩn của đường hồi quy được cho bởi công thức sau: Y = β₀ + β₁X
Hình 3 – Đường hồi quy
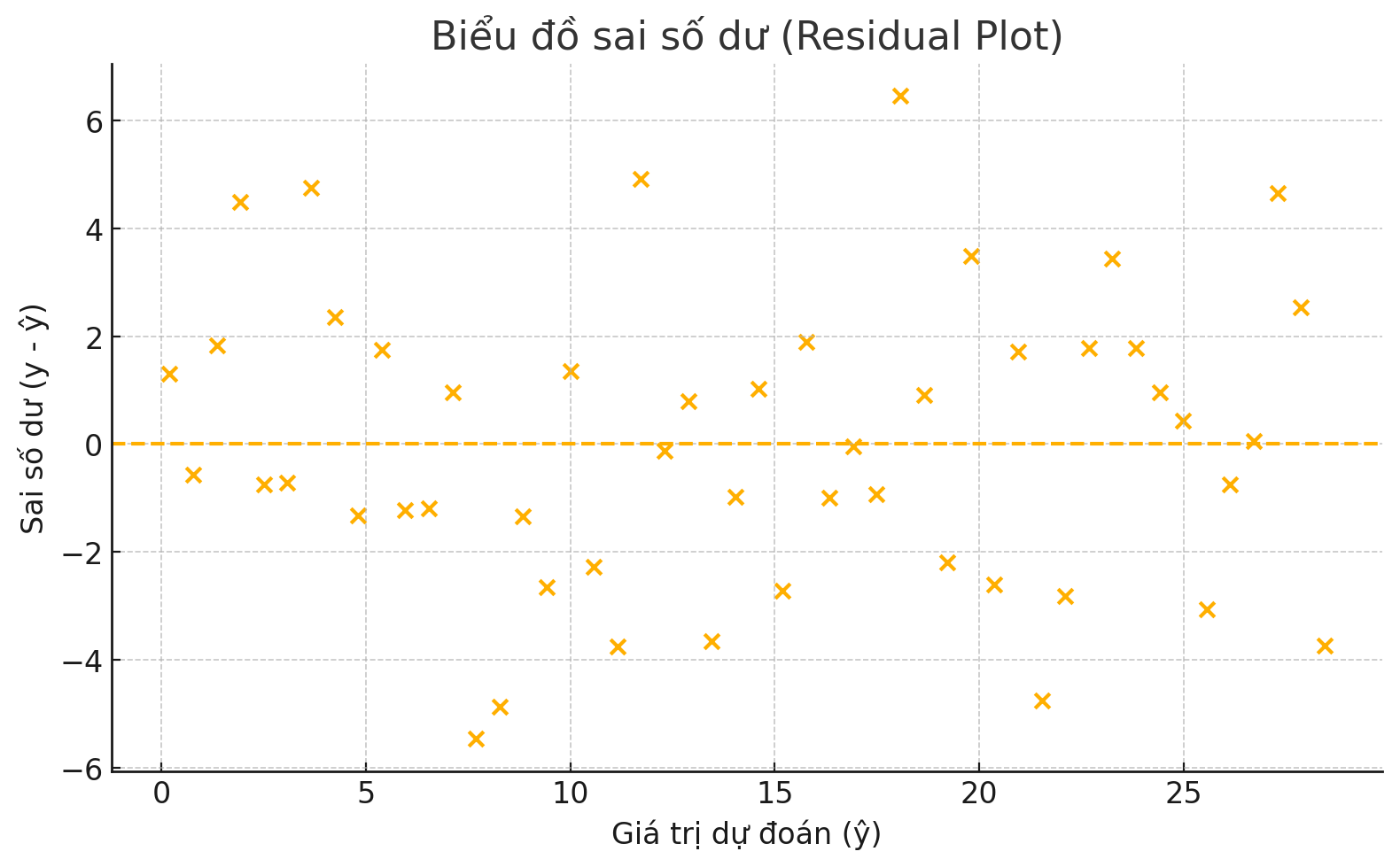
Đường thẳng khớp tốt nhất được tìm bằng cách tối thiểu hóa biểu thức RSS (Residual Sum of Squares - tổng bình phương sai số dư), vốn bằng tổng bình phương phần dư của mỗi điểm dữ liệu trên đồ thị. Sai số dư cho bất kỳ một điểm dữ liệu nào được tính bằng cách lấy giá trị thực tế của biến phụ thuộc trừ đi giá trị dự đoán của biến phụ thuộc đó:
Hình 4 – Sai số dư
Mức độ phù hợp của mô hình hồi quy tuyến tính có thể được đánh giá bằng 2 thước đo:
R² hay hệ số xác định (Coefficient of Determination)
Sai số chuẩn của phần dư (Residual Standard Error - RSE)
R² (Hệ số xác định)
Bạn cũng đã học một cách khác để kiểm tra độ chính xác của mô hình, đó là thống kê R². R² là một số cho biết tỷ lệ phần biến thiên của dữ liệu được giải thích bởi mô hình. Giá trị của R² luôn nằm trong khoảng từ 0 đến 1. Nói một cách tổng quát, nó cung cấp thước đo mức độ mà các kết quả thực tế được mô phỏng lại tốt bởi mô hình, dựa trên tỷ lệ phần trăm của tổng biến thiên của kết quả được mô hình giải thích (tức là kết quả kỳ vọng). Nhìn chung, R² càng cao thì mô hình của bạn càng phù hợp với dữ liệu.
Về mặt toán học, R² được biểu diễn như sau: R² = 1 - (RSS / TSS)
Hình 5 – R bình phương
RSS (Residual Sum of Squares - tổng bình phương sai số dư): Trong thống kê, RSS được định nghĩa là tổng sai số trên toàn bộ mẫu. Nó đo lường sự khác biệt giữa kết quả dự đoán và kết quả thực tế. RSS nhỏ cho thấy mô hình khớp rất chặt với dữ liệu. RSS cũng được định nghĩa như sau:
TSS (Total Sum of Squares - tổng bình phương sai số toàn phần): TSS là tổng các sai số của các điểm dữ liệu so với giá trị trung bình của biến đáp ứng. Về mặt toán học, TSS được tính như sau:
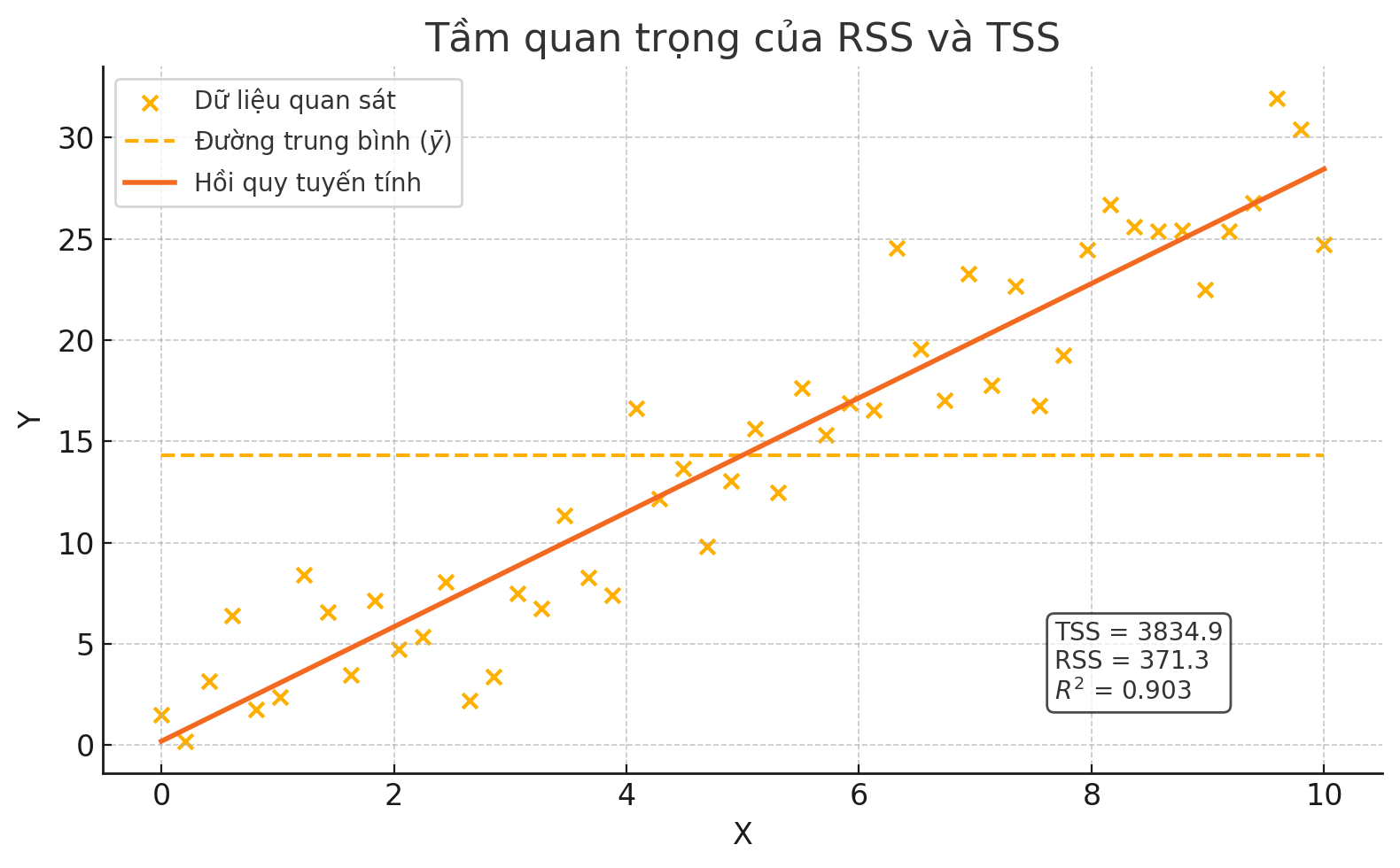
Tầm quan trọng của RSS/TSS:
Hãy suy nghĩ về điều này một chút. Nếu bạn không biết gì về hồi quy tuyến tính nhưng vẫn phải vẽ một đường thẳng để biểu diễn các điểm dữ liệu đó, cách đơn giản nhất bạn có thể làm là vẽ một đường thẳng đi qua giá trị trung bình của tất cả các điểm, như minh họa bên dưới.
Đây là cách xấp xỉ tệ nhất mà bạn có thể làm. TSS cho chúng ta độ lệch của tất cả các điểm so với đường trung bình.
Để củng cố trực quan hiểu biết này về R², bạn có thể xem 4 biểu đồ dữ liệu marketing và so sánh các giá trị R² tương ứng.
Biểu đồ 1: Tất cả các điểm nằm trên đường thẳng và giá trị R² đạt mức hoàn hảo là 1.
Biểu đồ 2: Một số điểm lệch khỏi đường thẳng và sai số thể hiện qua giá trị R² thấp hơn, ở mức 0,70.
Biểu đồ 3: Độ lệch tăng lên và giá trị R² giảm xuống còn 0,36.
Biểu đồ 4: Độ lệch còn lớn hơn nữa với giá trị R² rất thấp là 0,05.
Hồi quy tuyến tính đơn biến trong Python
Trong phần này, bạn đã tìm hiểu thêm một số khía cạnh lý thuyết về hồi quy tuyến tính đơn biến bên cạnh việc triển khai nó trong Python.
Nhìn theo hướng thống kê hơn:
Trong hồi quy tuyến tính, tại mỗi giá trị X, mô hình cho ra ước lượng tốt nhất cho Y.
Tại mỗi giá trị X, tồn tại một phân phối các giá trị của Y.
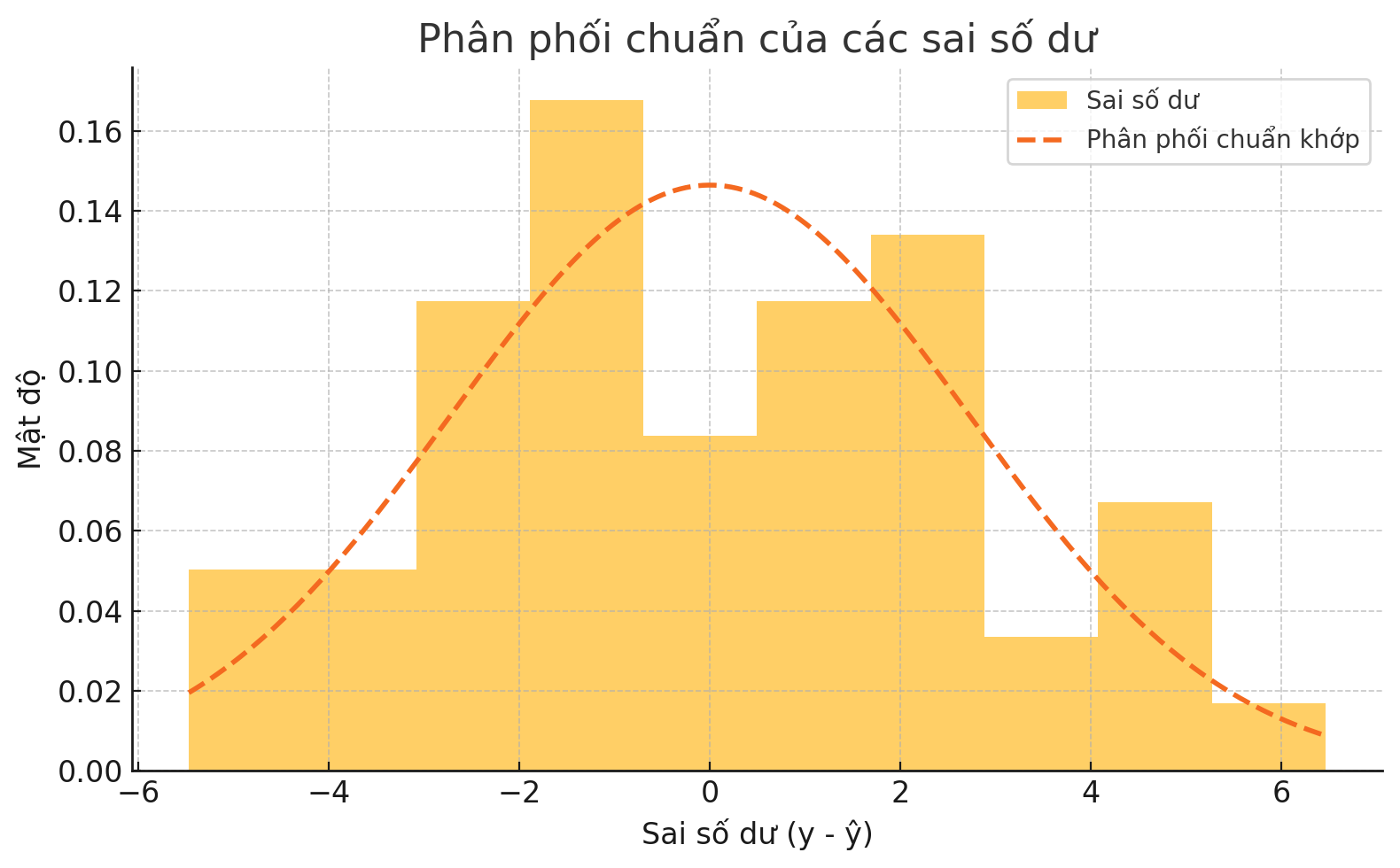
Mô hình dự đoán một giá trị đơn lẻ, do đó tồn tại một phân phối của các sai số tại mỗi giá trị dự đoán này, như có thể thấy ở hình bên dưới.
Hình 8 – Phân phối chuẩn của các sai số dư
Chúng ta hãy xem các giả định của hồi quy tuyến tính đơn biến là gì:
Mối quan hệ tuyến tính giữa X và Y.
Các sai số (phần dư) có phân phối chuẩn (lưu ý: giả định này không áp dụng cho X hay Y).
Các sai số độc lập với nhau.
Các sai số có phương sai không đổi (đồng nhất phương sai).
Với những giả định này, chúng ta có thể tiến hành suy luận về mô hình – điều mà nếu không có các giả định thì chúng ta đã không thể thực hiện. Cũng cần lưu ý rằng không hề có giả định nào về phân phối của X hay Y, chỉ có yêu cầu các sai số phải có phân phối chuẩn.
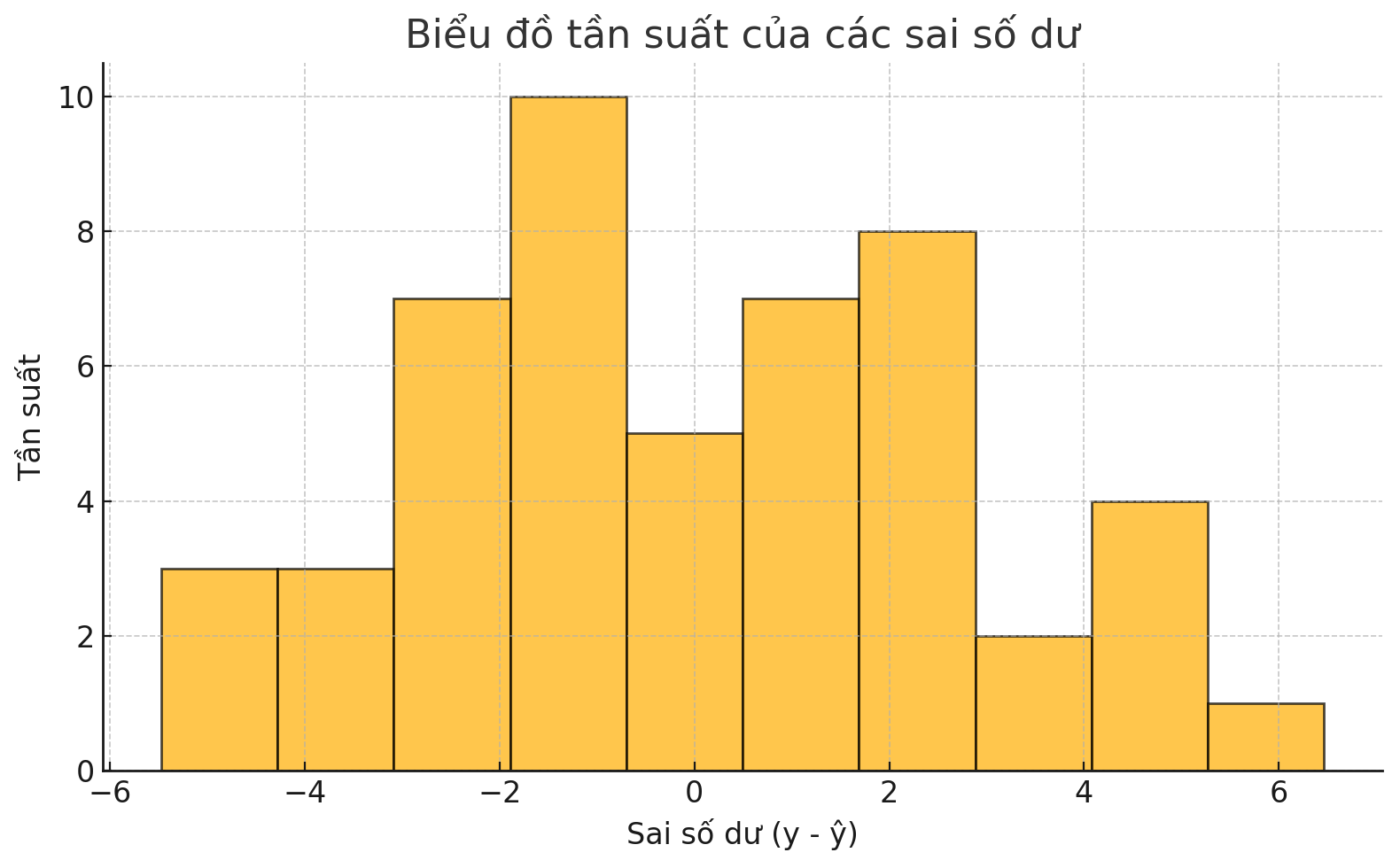
Giả định rằng các sai số có phân phối chuẩn là một giả định cực kỳ quan trọng khi chúng ta muốn suy luận từ mô hình hồi quy tuyến tính. Vì thế, việc phân tích các sai số dư này là rất quan trọng trước khi bạn tiến hành các bước tiếp theo. Phương pháp đơn giản nhất để kiểm tra tính chuẩn của phân phối sai số dư là vẽ biểu đồ tần suất của các sai số và xem liệu các sai số có phân phối chuẩn hay không.
Hình 9 – Biểu đồ tần suất của các sai số dư
Ngoài ra, bạn cũng cần kiểm tra xem có những mô hình (xu hướng) rõ rệt nào trong các sai số dư hay không, nhằm xác định rằng các sai số này có phương sai không đổi.
Hình 10 – Kiểm tra sự tồn tại của mô hình trong các sai số dư
Như bạn có thể thấy ở hình trên, hai biểu đồ đầu tiên rõ ràng thể hiện một kiểu mô hình nhất định, nhưng đến biểu đồ thứ ba, các sai số dư chỉ đơn thuần là nhiễu được phân bố đồng đều xung quanh giá trị 0 – đó là trường hợp lý tưởng.
Tóm tắt: Phân phối t là gì?
Đối với kích thước mẫu nhỏ, phân phối t có độ phân tán lớn hơn so với phân phối chuẩn.
Đối với kích thước mẫu lớn, phân phối t trở nên tương tự như phân phối chuẩn.
Thực chất, phân phối t chính là phân phối chuẩn được điều chỉnh để xét đến trường hợp kích thước mẫu nhỏ.
Sau khi bạn đã khớp một đường thẳng trên dữ liệu, cần đặt câu hỏi: “Liệu đường thẳng này có thật sự phù hợp một cách có ý nghĩa đối với dữ liệu hay không?” Hay nói cách khác, liệu hệ số β của đường hồi quy có ý nghĩa thống kê đến mức nó góp phần giải thích phương sai trong dữ liệu hay không?
Rõ ràng, bạn cần thực hiện kiểm định giả thuyết đối với hệ số β này. Giả thuyết không (H₀) và giả thuyết đối (H₁) trong trường hợp này là:
H₀: β₁ = 0 (hệ số β không có ảnh hưởng đến Y)
H₁: β₁ ≠ 0 (hệ số β có ảnh hưởng đáng kể đến Y)
Giả sử mô hình hồi quy tuyến tính đơn Y = β₀ + β₁X + ε, với n quan sát.
Ước lượng hệ số
β̂₁ = Σ[(Xᵢ − X̄)(Yᵢ − Ȳ)] ⁄ Σ(Xᵢ − X̄)²
Ước lượng phương sai sai số
s² = Σ eᵢ² ⁄ (n − 2), trong đó eᵢ = Yᵢ − Ŷᵢ
Sai số chuẩn của β̂₁
SE(β̂₁) = s ⁄ √Σ(Xᵢ − X̄)²
Thống kê kiểm định t
t = (β̂₁ − 0) ⁄ SE(β̂₁)
(Số 0 trong tử số là giá trị giả thuyết H₀: β₁ = 0)
Thống kê t này tuân theo phân phối t-Student với (n − 2) bậc tự do. So sánh |t| với giá trị tới hạn t_{α/2,(n−2)} (hoặc tính p-value) để quyết định bác bỏ hay không bác bỏ H₀:
Nếu |t| > t_{α/2,(n−2)} (hoặc p < α) → bác bỏ H₀, kết luận β₁ có ảnh hưởng đáng kể đến Y.
Ngược lại → chưa đủ bằng chứng để khẳng định β₁ ảnh hưởng đến Y.
Thống kê kiểm định này tuân theo phân phối t của Student với (n-2) bậc tự do. Sau đó, giá trị p được tính dựa trên thống kê kiểm định này để xác định xem hệ số hồi quy có ý nghĩa hay không.
Sau khi bạn xác định rằng hệ số hồi quy có ý nghĩa thống kê (dựa vào giá trị p), bạn cần sử dụng một số thước đo khác để đánh giá liệu độ phù hợp tổng thể của mô hình có ý nghĩa hay không. Để làm điều đó, bạn cần xem xét một tham số gọi là thống kê F.
Như vậy, các tham số để đánh giá một mô hình bao gồm:
Thống kê t: Dùng để xác định giá trị p, qua đó đánh giá liệu hệ số hồi quy có ý nghĩa hay không.
Thống kê F: Dùng để đánh giá liệu độ phù hợp tổng thể của mô hình có ý nghĩa hay không. Thông thường, giá trị thống kê F càng cao thì mô hình càng phù hợp (có ý nghĩa) hơn.
R²: Sau khi đã kết luận rằng độ phù hợp của mô hình là có ý nghĩa, giá trị R² cho biết mức độ phù hợp đó, tức là đường thẳng hồi quy diễn tả tốt như thế nào phương sai trong dữ liệu. Giá trị R² nằm trong khoảng từ 0 đến 1, với 1 là mức phù hợp tốt nhất và 0 là mức tệ nhất.
Hãy chắc chắn rằng bạn cũng xem lại phần hồi quy tuyến tính đơn biến trong Python từ các sổ tay (notebook) đã được cung cấp.
Hồi quy tuyến tính đa biến
Hồi quy tuyến tính đa biến là một kỹ thuật thống kê nhằm tìm hiểu mối quan hệ giữa một biến phụ thuộc và nhiều biến độc lập. Mục tiêu của hồi quy đa biến là tìm ra một phương trình tuyến tính có thể xác định tốt nhất giá trị của biến phụ thuộc Y dựa trên các giá trị khác nhau của các biến độc lập trong X.
Xét lại ví dụ trước đây của chúng ta về dự đoán doanh số dựa trên ngân sách marketing cho TV. Trong tình huống thực tế, trưởng phòng marketing sẽ muốn xem xét sự phụ thuộc của doanh số vào ngân sách được phân bổ cho các kênh marketing khác nhau. Ở đây, chúng ta xét ba kênh marketing khác nhau: marketing trên TV, marketing trên radio và marketing trên báo. Bạn cần xem xét nhiều biến vì chỉ một biến đơn lẻ có thể không đủ để giải thích biến mục tiêu, trong trường hợp này là doanh số.
Bảng dưới đây cho thấy việc thêm một biến đã giúp tăng giá trị R² mà chúng ta thu được khi chỉ sử dụng biến TV.
| Mô hình | Biến đầu vào được sử dụng | R² (Giải thích phương sai) | Thay đổi R² so với mô hình trước | Ghi chú ngắn gọn |
|---|---|---|---|---|
| 1. TV | TV | 0,61 | – | Quảng cáo TV một mình giải thích khoảng 61 % biến thiên doanh số. |
| 2. TV + Radio | TV, Radio | 0,90 | + 0,29 | Thêm ngân sách Radio giúp mô hình giải thích thêm 29 % phương sai. |
| 3. TV + Radio + Báo | TV, Radio, Báo (Newspaper) | 0,91 | + 0,01 | Báo in chỉ cải thiện rất nhỏ; hai kênh TV & Radio đã nắm gần hết tín hiệu. |
Như vậy, chúng ta thấy rằng việc thêm nhiều biến hơn làm tăng giá trị R² và có thể là một ý tưởng tốt khi sử dụng nhiều biến để giải thích một biến mục tiêu. Về cơ bản:
Việc thêm các biến đã giúp bổ sung thông tin về phương sai của Y!
Nhìn chung, chúng ta kỳ vọng khả năng giải thích của mô hình sẽ tăng khi số lượng biến tăng.
Do đó, chúng ta đi đến hồi quy tuyến tính đa biến, vốn chỉ là một mở rộng của hồi quy tuyến tính đơn biến.
Công thức thiết lập mô hình hồi quy tuyến tính đa biến cũng tương tự như hồi quy tuyến tính đơn biến, với thay đổi nhỏ là thay vì chỉ có một hệ số β cho một biến, giờ đây bạn sẽ có nhiều hệ số β cho tất cả các biến được sử dụng. Công thức lúc này có thể được viết đơn giản như sau:
Ngoài công thức, nhiều ý tưởng khác trong hồi quy tuyến tính đa biến cũng tương tự như hồi quy tuyến tính đơn biến, chẳng hạn như:
Mô hình bây giờ khớp một "siêu mặt phẳng" thay vì một đường thẳng.
Các hệ số hồi quy vẫn được tìm bằng cách tối thiểu hóa tổng bình phương sai số (theo tiêu chí bình phương tối thiểu).
Về suy luận, các giả định từ hồi quy tuyến tính đơn vẫn giữ nguyên hiệu lực:
Sai số có kỳ vọng bằng 0, độc lập, phân phối chuẩn và có phương sai không đổi.
Phần suy luận trong hồi quy tuyến tính đa biến nhìn chung vẫn tương tự như trong hồi quy đơn biến.
Mặc dù hầu hết các ý tưởng trong hồi quy tuyến tính đơn và đa biến là giống nhau, vẫn có một vài cân nhắc mới mà bạn cần lưu ý khi chuyển sang hồi quy tuyến tính đa biến, chẳng hạn như:
Thêm nhiều biến chưa chắc lúc nào cũng có ích:
a. Mô hình có thể "quá khớp" (overfit) khi trở nên quá phức tạp.
i. Mô hình khớp với tập huấn luyện quá tốt nhưng không tổng quát hóa tốt sang dữ liệu kiểm tra.
ii. Dấu hiệu: độ chính xác trên tập huấn luyện cao, nhưng độ chính xác trên tập kiểm tra thấp.
b. Đa cộng tuyến (multicollinearity).
i. Các biến độc lập có sự tương quan lẫn nhau.Việc chọn lựa đặc trưng (feature) trở thành một khía cạnh quan trọng.
Chúng ta hãy xem xét từng cân nhắc mới này một cách chi tiết:
Quá khớp (Overfitting): Khi bạn thêm ngày càng nhiều biến vào mô hình – ví dụ, giả sử bạn không ngừng tăng bậc của một hàm đa thức để khớp dữ liệu – mô hình của bạn có thể kết thúc bằng việc “nhớ” toàn bộ các điểm dữ liệu trong tập huấn luyện. Điều này sẽ gây ra vấn đề nghiêm trọng cho khả năng khái quát hóa; nghĩa là, khi mô hình chạy trên dữ liệu kiểm tra, độ chính xác sẽ giảm mạnh vì mô hình không tổng quát hóa tốt. Đây là biểu hiện kinh điển của việc mô hình bị quá khớp.
Đa cộng tuyến (Multicollinearity): Đa cộng tuyến là hiện tượng các biến dự báo có mối quan hệ với nhau trong mô hình hồi quy tuyến tính đa biến. Nói đơn giản, trong một mô hình được xây dựng với nhiều biến độc lập, một số biến có thể liên hệ với nhau, tức là một số biến có thể hoàn toàn giải thích cho một biến độc lập khác trong mô hình, khiến sự có mặt của biến đó trong mô hình trở nên dư thừa. Vì vậy, để biết ảnh hưởng lên biến mục tiêu đến từ đâu, chúng ta cần loại bỏ một số biến độc lập có liên quan này. Về cơ bản, đa cộng tuyến ảnh hưởng đến:
Khả năng diễn giải: Liệu "sự thay đổi của Y khi giữ cố định các biến khác" có còn đúng nữa hay không?
Suy luận thống kê:
a. Các hệ số hồi quy dao động mạnh, dấu của chúng có thể bị đảo lộn.
b. Do đó, các giá trị p trở nên không đáng tin cậy.
Tuy nhiên, có một số khía cạnh mà đa cộng tuyến không ảnh hưởng tới, chẳng hạn như:
a. Các dự đoán và độ chính xác của các dự đoán.
b. Các thống kê độ phù hợp của mô hình như R².
Do đó, việc xử lý đa cộng tuyến là cực kỳ quan trọng. Có hai cách để phát hiện đa cộng tuyến trong một mô hình:
Tương quan: Xem xét tương quan từng cặp giữa các biến độc lập đôi khi có thể hữu ích để phát hiện đa cộng tuyến.
Hình 13 – Tương quan từng cặp
Từ các hình trên (vẽ cho bộ dữ liệu iris), bạn có thể thấy rõ rằng một số cặp biến, chẳng hạn như chiều rộng cánh hoa và chiều dài đài hoa, chiều rộng cánh hoa và chiều dài cánh hoa, v.v., có tương quan cao với nhau. Do đó, khi mô hình được xây dựng, một trong các biến từ mỗi cặp biến này có thể trở nên dư thừa đối với mô hình.
Hệ số phóng đại phương sai (Variance Inflation Factor - VIF): Tuy nhiên, việc chỉ nhìn vào tương quan chưa chắc lúc nào cũng hữu ích, vì có khả năng chỉ một biến thì không hoàn toàn giải thích được một biến khác, nhưng một số biến kết hợp lại có thể làm được điều đó. Để kiểm tra mối quan hệ kiểu này giữa các biến, chúng ta sử dụng VIF. VIF cơ bản giúp giải thích mức độ liên quan của một biến độc lập với tất cả các biến độc lập khác. Công thức tính VIF được cho bên dưới:
Công thức hệ số phóng đại phương sai (VIF)
trong đó
-
là chỉ số của biến độc lập đang xét.
-
là hệ số thu được khi hồi quy lên tất cả các biến độc lập còn lại trong mô hình.
Diễn giải:
-
càng cao ⇒ càng được “dự đoán” tốt bởi các biến khác ⇒ multicollinearity cao.
-
→ không có đa cộng tuyến đối với
-
(hoặc 10) → thường coi là đáng lo ngại, nên cân nhắc loại bớt hoặc biến đổi biến.
Kinh nghiệm thông thường đối với VIF là: nếu VIF lớn hơn 10 thì chắc chắn là cao, còn VIF lớn hơn 5 cũng không nên bỏ qua và cần được xem xét kỹ lưỡng.
Bây giờ, sau khi đã phát hiện có đa cộng tuyến trong mô hình, bạn cần xử lý nó một cách thích hợp để tránh xây dựng một mô hình phức tạp không cần thiết với nhiều biến dư thừa. Một vài phương pháp để xử lý đa cộng tuyến bao gồm:
Loại bỏ biến:
a. Bỏ biến có tương quan cao với các biến khác.
b. Chọn biến có ý nghĩa về mặt nghiệp vụ (nếu việc diễn giải và giải thích kết quả là quan trọng).Tạo biến mới bằng cách kết hợp các biến cũ:
a. Thêm các đặc trưng tương tác, tức là các đặc trưng được tạo ra từ một số đặc trưng gốc:
i. số phòng ngủ / số phòng tắm
ii. diện tích / số tầng
b. Biến đổi biến số:
i. PCA (sẽ được đề cập trong mô-đun sau).
Chuẩn hóa đặc trưng (Feature Scaling): Một khía cạnh quan trọng khác cần cân nhắc là việc chuẩn hóa các đặc trưng. Khi bạn có nhiều biến độc lập trong một mô hình, nhiều biến trong số chúng có thể có các thang đo rất khác nhau, điều này sẽ dẫn đến một mô hình có các hệ số rất kỳ lạ và khó diễn giải. Vì vậy, chúng ta cần chuẩn hóa các đặc trưng vì hai lý do:
Dễ dàng diễn giải.
Tăng tốc độ hội tụ cho các phương pháp hạ gradient.
Bạn có thể chuẩn hóa các đặc trưng bằng hai phương pháp rất phổ biến:
Chuẩn hóa Z-score (Standardizing): Các biến được chuyển đổi sao cho giá trị trung bình của chúng bằng 0 và độ lệch chuẩn bằng 1.
Chuẩn hóa Min-Max (MinMax Scaling): Các biến được chuyển đổi sao cho mọi giá trị của chúng nằm trong khoảng từ 0 đến 1, dựa trên giá trị lớn nhất và nhỏ nhất trong dữ liệu.
Điều quan trọng cần lưu ý là việc chuẩn hóa chỉ ảnh hưởng đến các hệ số hồi quy và không ảnh hưởng đến bất kỳ tham số nào khác như thống kê t, thống kê F, giá trị p, R², v.v.
Trong mô hình hồi quy tuyến tính đơn, bạn chỉ làm việc với các biến số kiểu số. Nhưng khi có nhiều biến, có thể sẽ xuất hiện một số biến phân loại (categorical) tỏ ra hữu ích cho mô hình. Vì vậy, việc xử lý thích hợp những biến này là rất cần thiết để có được một mô hình tốt. Một cách để xử lý các biến phân loại là tạo các biến giả (dummy variables). Ý tưởng chính khi tạo biến giả là: đối với một biến phân loại có n mức độ (levels), bạn sẽ tạo ra n-1 cột mới, mỗi cột biểu thị sự có mặt (1) hay không có mặt (0) của một mức độ tương ứng. Hãy xem ví dụ dưới đây để hiểu rõ hơn.
Hình 14 – Các biến giả